Physics

I was a postdoc working in Suzanne Fielding‘s group in the physics department at Durham until Jan 2018. There I studied a variety of fluid dynamics problems in soft matter, using a combination of analytical and numerical methods. The topics included active matter, flows in porous media, and contact line dynamics.

Snapshot from a simulation of active matter, showing a turbulent state. Red lines show the local orientation. Red/green circles show defects in the structure.

Active matter

There has been much recent interest in so called “active matter”, i.e., materials that are capable of powering themselves through a fluid using an internal fuel supply. Examples include shoals of fish, suspensions of swarming bacteria, or cell extracts that comprise of groups of molecular motors and long filaments. Many previous researchers have studied the stability and fluid dynamics of these types of materials in the presence of simple liquids such as water. However the biological environments in which these materials are typically found, e.g., in fluids such as mucus, are more complex. For example depending on the rate at which they are deformed, these materials can act as a liquid, an elastic solid, or somewhere in-between. As part of a international collaboration, I studied a new model that places active matter in a polymer fluid background. I looked at the stability of these materials analytically by checking for the response of the flow field to small disturbances, and then tested my predictions with 2D computer simulations. Our model reveals a rich array of fascinating behaviour, including oscillatory states and “active turbulence”.

publications:

E. J. Hemingway, P. Mishra, M. C. Marchetti, S. M. Fielding (2016). Soft Matter, 12, 7943 [pdf]

E. J. Hemingway, M. E. Cates, & S. M. Fielding (2016). Phys. Rev. E 93, 032702 [pdf]

E. J. Hemingway, A. Maitra, S. Banerjee, M. C. Marchetti, S. Ramaswamy, S. M. Fielding, & M. E. Cates (2015). Phys. Rev. Lett., 114, 098302 [pdf]

Contact line

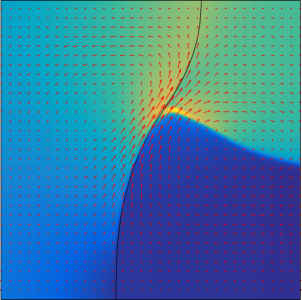
The point at which the interface between two fluids meets a solid wall is called the contact line. This underpins a wide range of phenomena in nature, e.g., it allows water beetles to collect water in the desert and allows water skaters to move. Understanding the physics of the contact line can lead to technological applications from oil recovery to and inkjet printing. The contact line moves when, e.g., a droplet rolls down a slope. However the Navier-Stokes equations, which describe fluid flow, normally prescribe that the fluid velocity is zero at any solid surface, posing an apparent contradiction. This project used 2D fluid mechanics simulations to look at how the contact-line moves, and what sets the size the “slip region” in which motion is accommodated. Our results provide criteria that must be satisfied to properly capture the physics of the slip region in any future simulations.

publications:

H. Kusumaatmaja, E. J. Hemingway, & S. M. Fielding (2016). J. Fluid Mech., 788, 209 [pdf]

Edge fracture

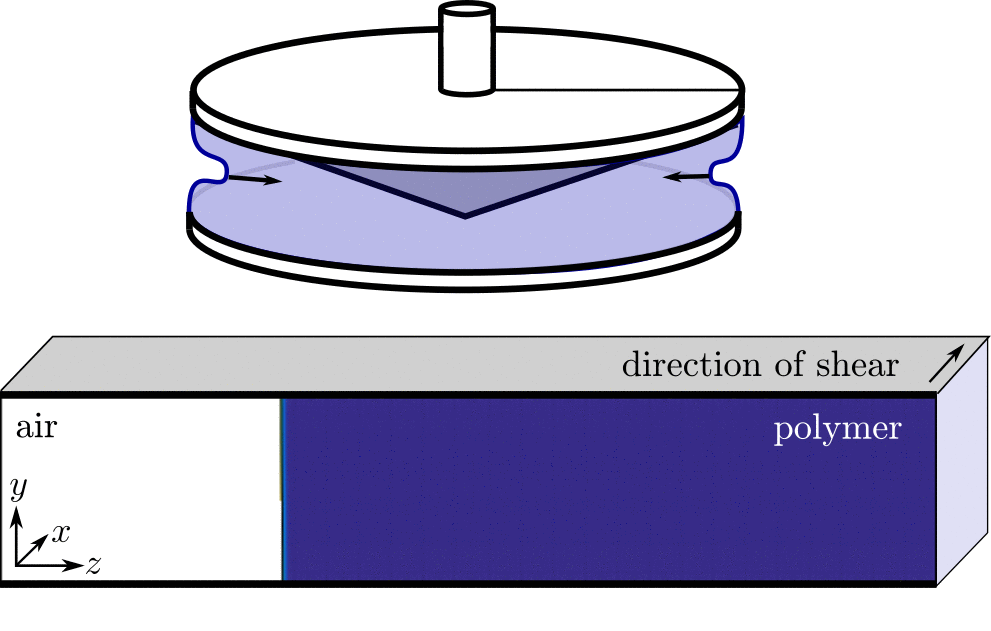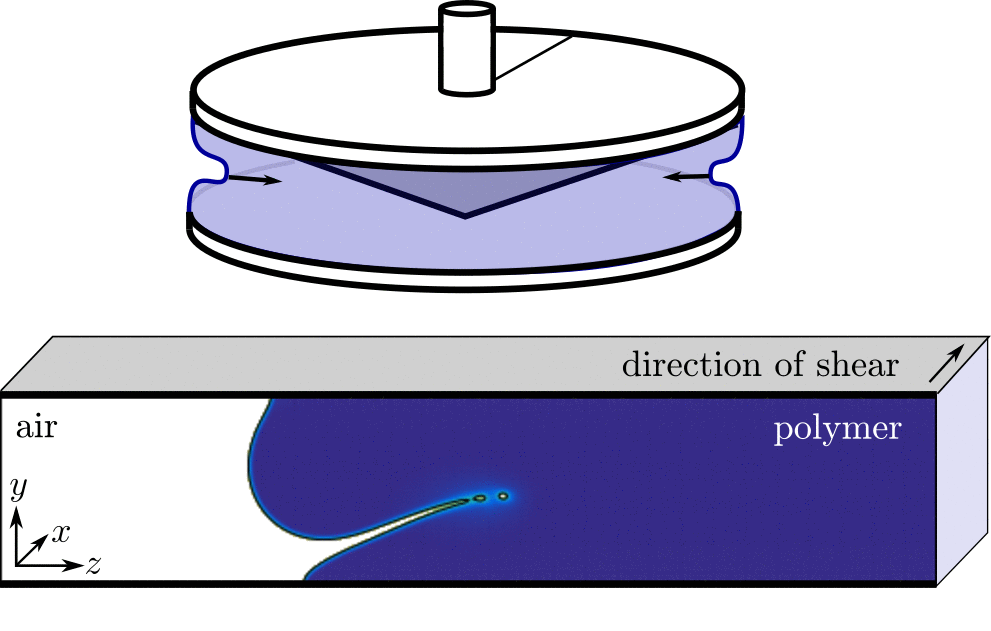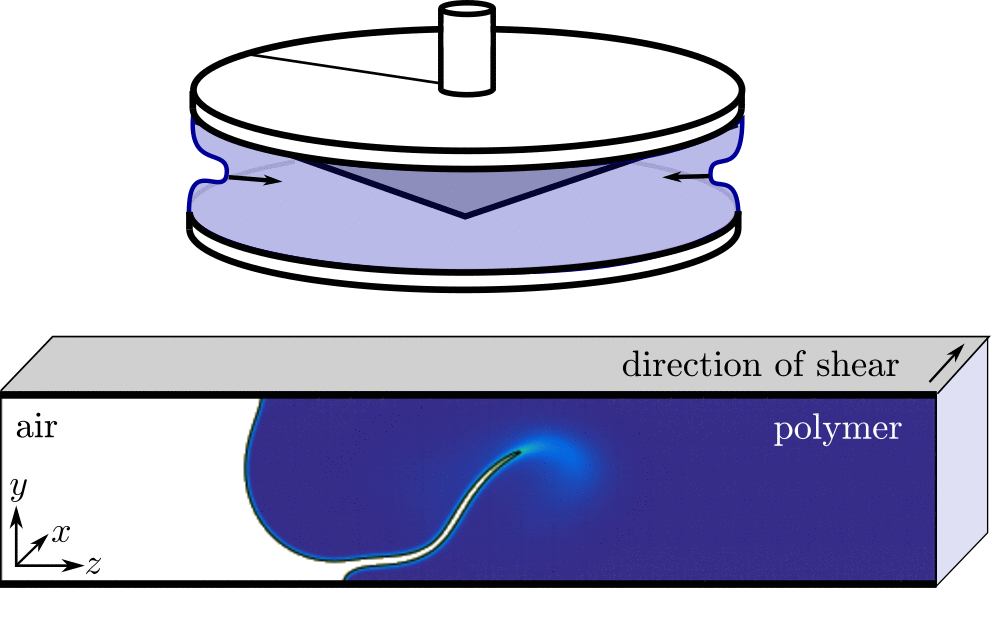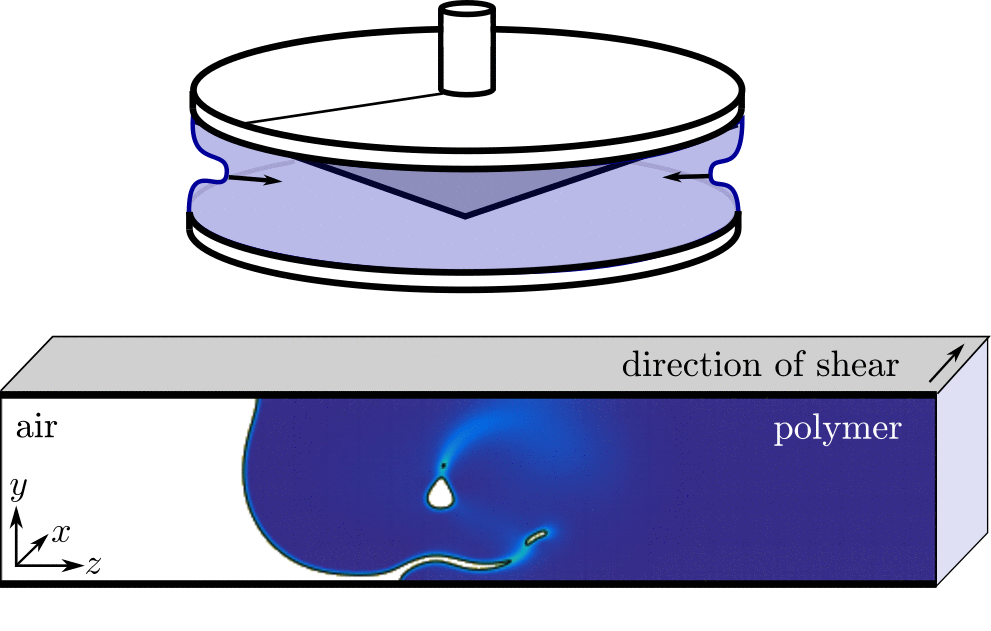
TBC

publications:

E. J. Hemingway, H. Kusumaatmaja, S. M. Fielding (2017). Phys. Rev. Lett., 119, 028006 [pdf]

E. J. Hemingway, S. M. Fielding, Edge-Induced Shear Banding in Entangled Polymeric Fluids. Physical Review Letters. 120 (2018), [pdf]

E. J. Hemingway, S. M. Fielding, Edge fracture instability in sheared complex fluids: Onset criterion and possible mitigation strategy. Journal of Rheology. 63 (2019) [pdf] [scilight]

E. J. Hemingway, S. M. Fielding, Interplay of edge fracture and shear banding in complex fluids. Journal of Rheology. 64 (2020) [pdf]